ハル研究所プログラミングコンテスト2020 参加記
ハル研究所プログラミングコンテスト2020に参加しました。結果は、総ターン数24,815で9位でした!
賞金圏内にはなれなかったけどランキングに載れてよかったです。せっかくなので自分の解法を書き残しておきます。
問題概要
"うさぎ"がステージ上にある複数の"巻物"をすべて取り終えるまでのターン数を最小化する問題。ステージは200個あり、最終的なスコアである総ターン数が小さいほど良い。
- ステージ
- 位置座標は
(float, float)で表現される - 全体の形状は1辺
の正方形 - 1辺
のマス目上に区切られ、各マスは4つの"地形"のいずれかが割り当てられている 〜 個の巻物が配置されている
- 位置座標は
- うさぎは、現在位置
に対して次を満たす位置 に移動可能:
:現在の巻物取得個数 :現在位置の地形に対応する補正値
- うさぎは、巻物が置かれているマスに入ったときにその巻物を取得する
Metric TSPに近いが、移動可能距離が各ターンの状態に依存することによって問題を複雑化している。また、地形の形状やターン数は整数で表現される一方でうさぎと巻物の位置は浮動小数点数で表現されることも特徴的。
大まかな解法
ハル研プロコン終了直前9位でした!
— Ark (@arkark_) November 18, 2020
やったこと:TSPをbit DPで計算。巻物間のパスはビームサーチで探索。途中で一度曲がるパスの必要ターン数で評価。
その他:Nearest Neighborで枝刈り。巻物取得位置をマスの角や辺に調整。いい感じの境界を二分探索。など
ソースコード
1 | tokei Answer.cpp |
開発環境
- ビルドツール:make
- エディタ:Visual Studio Code
- デバッガ:gdb
使用PCがubuntuでVisual Studioという選択肢がなかったので、makeを叩いてました。
イテレーションの自動化
「実装したあとにビューワを見る」という作業はコンテスト期間中に何度も行うことが予想できたので、最初にこの部分を自動化しました。
make viewと叩くだけで「ビルド → 実行 → JSONファイル出力 → ローカルサーバを起動[1] → ブラウザを起動 → ビューワを起動 → ファイル指定」をやってくれます。これだけでかなり作業効率が上がりました。その他便利コマンドをいくつか生やしました。
解法
全体の計算の流れは次のようになっています:
- 軽めの処理のビームサーチで うさぎ-巻物間 と 巻物-巻物間 の必要ターン数を計算する。
- bit DPで巻物の取得する順番を決める。
- その順番に対して重めの処理のビームサーチを実行して、より精度の良い経路を計算する。
- 3.で求めた経路に局所的な改善が可能な場合は、経路を補正する。
bit DPで巻物を取る順番を決める
現時点での巻物取得数が
計算の高速化:
- メモ化:bit DP中に同じ2点間の計算をしない。
- 計算の省略:すべての取得済み巻物数に対して計算するのは大変なので、うさぎのジャンプ力の比を考慮しながら適当に計算をサボる。ソースコードではこの部分。
- Nearest Neighborを先に計算しておき、枝刈り。
ビームサーチで2点間の経路を決める
地形効果によって、目的地へまっすぐ進むより迂回したほうが良いケースがたくさんあります。この「迂回」をどのように実現するかに悩みましたが、以下の方法で取り組みました。
基本的にビームサーチによる方針です[2]。
今、点
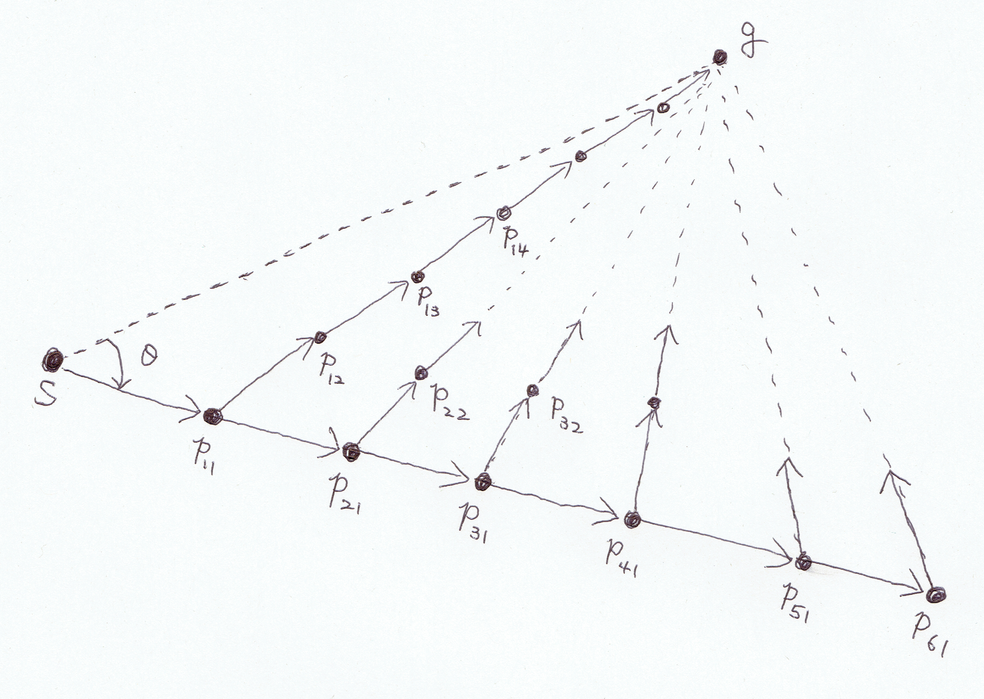
ここで
は直感的に、最初の方向を
この遷移は各
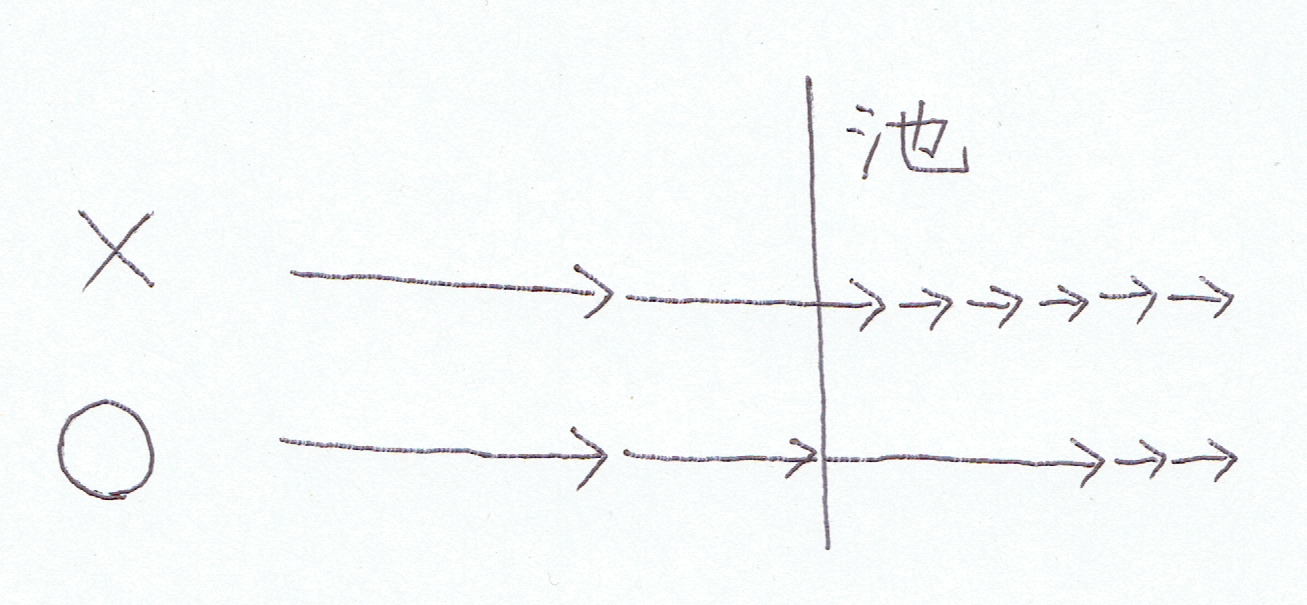
悪路に入りそうな場合に"次の位置"を補正する
悪路に入る(例えば移動前と移動後で地形が平地から池へ変化)移動に対して、下図のように悪路手前で一度止めるヒューリスティックをまず考えました。
さらに、単純に移動距離を短くするのではなく、下図のように、移動距離を保ったまま方向ベクトルを回転させてぎりぎりの境界になる場所に変更するヒューリスティックを考えました。コードではこの部分です。境界は二分法[3]で求めています。
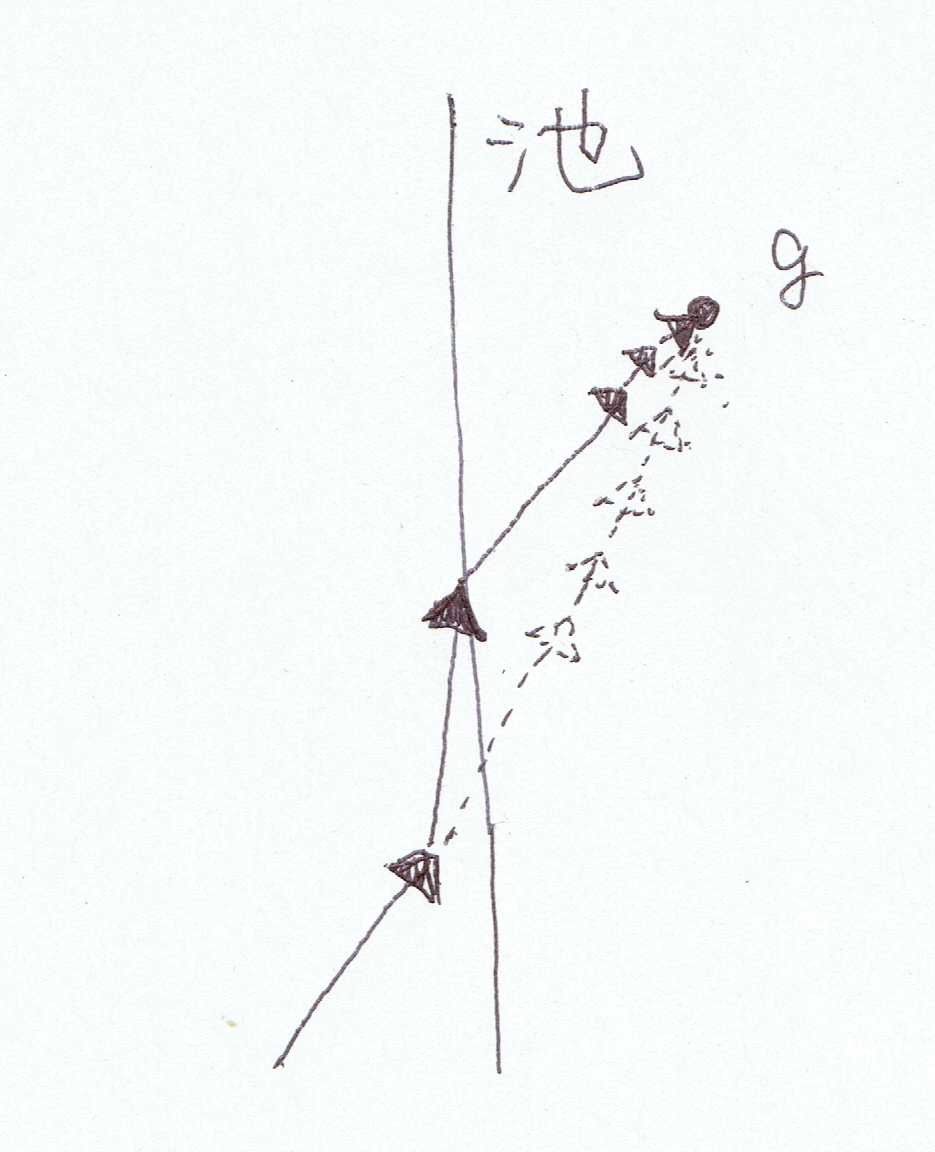
こうすると、単純に手前で止めるよりスコアの改善度合いが良かったです。
"次の位置"の補正はビームサーチの遷移計算時に行っています。回転による補正の方は、二分法による
巻物の取得位置をマスの中央からずらす
巻物の取得判定はうさぎが同一マスにいることなので、例えばマスの角で取得したほうが良いケースが多くあります。
実際には、各巻物のいるマスの中央を始点とした軽めのビームサーチで求めた経路の最初の方向ベクトルに向けて、取得位置をずらしました。コードではこの部分が該当します。
経路を局所最適化する
重めのビームサーチによる経路計算後に、局所的な経路改善を行いました。例えば、経路
その他、高速化やヒューリスティック
以上の解法は時間をかなり使うため、色々高速化をしました。実際よりも結果が悪くなるが致し方なく計算をサボっているところもたくさんあります。
また、文章では伝えられない細かいお気持ちヒューリスティックがコードのあちこちに散らばっています。
スコアの推移
コミット履歴を見たところ以下のようなスコア遷移でした。
高速化によってスコアが上がってるのは、探索に回せる時間が増えたためです。
| 実装したもの | Local Score | Remote Score |
|---|---|---|
| 2点間の経路を直線のみにしてTSP | 48,329 | N/A |
| ビームサーチの実装(+高速化) | 27,696 | 28,141 |
| 悪路に入る場合は手前で止める | 27,311 | 27,762 |
| Nearest NeighborでTSPを枝刈り | 26,174 | 26,569 |
| 巻物取得位置の調整 | 25,674 | 25,972 |
| 回転による位置補正 | 25,140 | 25,700 |
| 色々高速化+ヒューリスティック | 24,663 | 25,303 |
| TSPの計算をサボるときにジャンプ力の比を考慮 | 24,430 | 25,047 |
| ヒューリスティック+パラメータチューニング | 24,387 | 24,815 |
感想
問題に関して
ハル研プロコンの例年の問題は「一見単純な問題設定に見えて、いざ考察すると非常に悩ませる且つ色々なアプローチが存在する」という性質があると思うのですが、今年の問題は特にその性質を強く感じました。連続と離散が混在することが原因で、考察難易度と実装難易度がともに跳ね上がってました。そのおかげで解きごたえがあり非常に楽しめました。
実際、「観察する → アイデアを思いつく → 実装する → 改善する」のフローがたくさん発生しました。長期プロコンならではの楽しさが そこには詰まってました。
ランキングに関して
今年は1位の人が序盤から1位を独走し続けていたため、「今の自分の解法はここからさらに
また、最終日付近でのスコア・順位の変動が激しかったのも印象的でした。Twitterでのみんなの反応も含め楽しかったです。
解法に関して
上位陣の解法を見ると、自分のアプローチとは異なっていて、いい感じのグラフを構築して最短経路問題を解いている人が多い印象でした。考察中にその方針を思いつかなかったのはまだまだ未熟だったなあと反省してます。一方で、他の人とは異なる方法で上位に食い込められたのはそれはそれで嬉しいです。
最後に
お約束ですが、こんなに楽しいプロコンの作問・運営をありがとうございました。もうハル研プロコンには参加できないですが、来年以降も期待しています。